So the whole point of MATLAB is not to be a large calculator - it is to program. A key aspect of programming is to create variables - things that we can store information in or compute - and manipulate them.
Let's try the following classic variable assignment. Type the following into MATLAB, one line at a time:
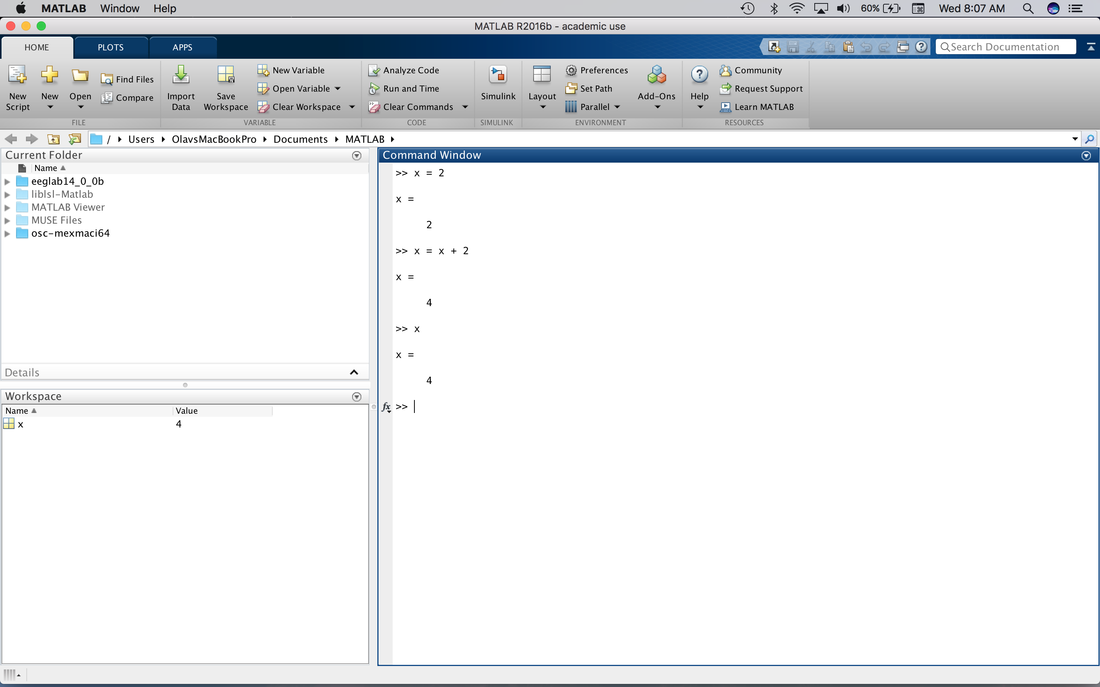
x = 2
x = x + 2
x
You should see the following:
Let's try the following classic variable assignment. Type the following into MATLAB, one line at a time:
x = 2
x = x + 2
x
You should see the following:
So, what has happened here? You first created a variable called x and gave it a value of 2. In most programming languages, this is called assignment. The thing on the left, "x", is equal to, or assigned, the value on the right, 2.
Next, you now said x, which was equal to 2, is equal to x (2) + 2, thus 4. Make sense? You will also see that the Workspace has a variable in it called x with a value of 4 when this is all over.
EXPERT NOTE. In some programming languages, you have to declare variables before you assign them. In MATLAB, you can do this but typically we assign them on the fly (as we create them).
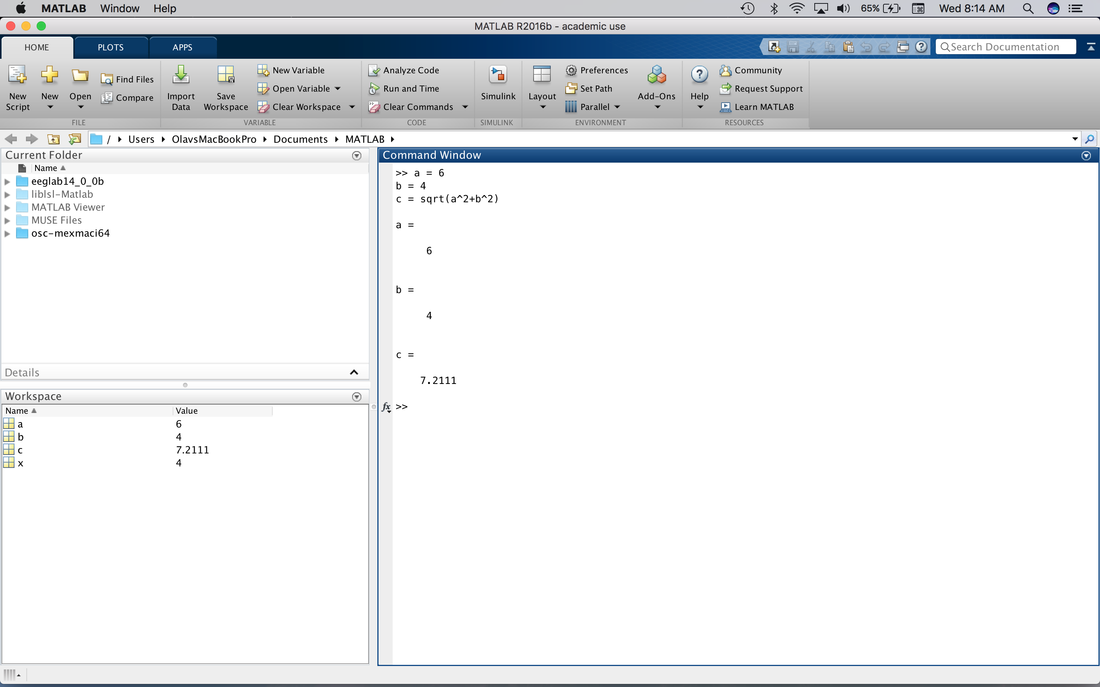
Now, for a more advanced exercise on this try the following. Imagine you have two sides of a right triangle, a, the opposite side with a value of 6 and b, the adjacent side with a value of 4. What is the length of the hypotenuse?
Well, one way to do this is with Pythagorus - a^2 + b^2 = c^2. So, c would be equal to the square root of a squared plus b squared. So, in MATLAB:
a = 6
b = 4
c = sqrt(a^2+b^2)
You should see the following:
Next, you now said x, which was equal to 2, is equal to x (2) + 2, thus 4. Make sense? You will also see that the Workspace has a variable in it called x with a value of 4 when this is all over.
EXPERT NOTE. In some programming languages, you have to declare variables before you assign them. In MATLAB, you can do this but typically we assign them on the fly (as we create them).
Now, for a more advanced exercise on this try the following. Imagine you have two sides of a right triangle, a, the opposite side with a value of 6 and b, the adjacent side with a value of 4. What is the length of the hypotenuse?
Well, one way to do this is with Pythagorus - a^2 + b^2 = c^2. So, c would be equal to the square root of a squared plus b squared. So, in MATLAB:
a = 6
b = 4
c = sqrt(a^2+b^2)
You should see the following:
Helpful Hint. The Workspace can get crowded. To empty it, you do not use clc, that clears the Command Window. To clear the Workspace we use clear all. Try this now.
To make sure we get the concept of variable assignment, let's try to solve the problem above with trigonometry. If you recall your maths we can find the angle in question by using the arc tangent. Note, the formula for atan has a d on the to specify degrees; if we had of just used atan the angle would be in radians. You will notice we left the semicolon off of the end of these lines.
angle = atand(6/4)
Then we can use the sind equation to find the hypotenuse.
hypotenuse = 6/sind(angle)
Repeat these two lines with the semicolon and you will notice that the answers are not displayed in the Command window. First however, clear the Workspace by using clc and clear all variables by using clear all.
clc
clear all
angle = atand(6/4);
hypotenuse = 6/sind(angle);
Note, there are many different types of variables in MATLAB. You will see a lot of them in the coming tutorials.
To make sure we get the concept of variable assignment, let's try to solve the problem above with trigonometry. If you recall your maths we can find the angle in question by using the arc tangent. Note, the formula for atan has a d on the to specify degrees; if we had of just used atan the angle would be in radians. You will notice we left the semicolon off of the end of these lines.
angle = atand(6/4)
Then we can use the sind equation to find the hypotenuse.
hypotenuse = 6/sind(angle)
Repeat these two lines with the semicolon and you will notice that the answers are not displayed in the Command window. First however, clear the Workspace by using clc and clear all variables by using clear all.
clc
clear all
angle = atand(6/4);
hypotenuse = 6/sind(angle);
Note, there are many different types of variables in MATLAB. You will see a lot of them in the coming tutorials.