How To Do Bayesian T-TEST in R
How To Run a Bayesian Analysis in R using the BEST package
1. OSX users. You need to install the latest version of XCode from the App store. Note, you will need to run XCode and accept the user agreement before you go any further.
2. Install R on your computer. Go to: http://cran.stat.sfu.ca/ and select the correct version for your operating system.
3. Install R Studio on your computer. Go to: https://www.rstudio.com/products/rstudio/download/
4. Install “jags” – this is a program that the BEST package needs in order to do some of the probability mathematics. Go to: http://sourceforge.net/projects/mcmc-jags/files/JAGS/4.x/
5. Open R. You should get to a command window. I have found that installing packages in R as opposed to R Studio leads to considerably greater success.
6. At the command “>” type in “install.packages(‘rjags’)” and hit enter. This will install the “rjags” package that you will need for BEST. Note, you will most likely see R installing a bunch of other packages that “rjags” needs to work. This is normal and okay.
7. At the command “>” type in “install.packages(‘BEST’)” and hit enter. This will install the “BEST” package. Note, you will most likely see R installing a bunch of other packages that “BEST” needs to work. This is normal and okay.
8. Create a directory called “R” on your desktop and put the attached sample data file, “data1.txt” in that directory (or a directory of your choice).
9. Open R Studio. (Note, this is not a full R tutorial, I will leave that for others).
10. At the command prompt, “>” type in “library(BEST)”. This tells R that you will be using the BEST library for some of your commands.
11. Next, change your working directory to the R directory in RStudio by typing “setwd("~/Desktop/R")” at the command prompt “>”.
12. Now, we will load in the sample data file (data1.txt). At the command prompt “>” type in “data1 = read.table("data1.txt")” to load the file data.txt into a structure that R calls a table. It's a matrix, but one specifically designed to work with statistical data. If you now simply type “data1” at the command prompt “>” you should see two columns (V1, V2) of 20 numbers.
13. To just look at a single column of numbers in R you isolate it by typing “data1$V1” for instance at the command prompt “>”.
14. Lets create the difference scores for this data. Type “difscores = data1$V2 – data1$V1” at the command prompt “>”. Check to see this works by typing “difscores” at the command prompt “>”.
15. As you can see, R is a bit like MATLAB or other programming environments. Anything on the left of an equals sign is an assigned variable and anything on the right is / are operations. For example, using a classic example if you type “x = 2 + 5” you will be creating a variable “x” that is equal to 7. In the original version of R “<-“ was used instead of “=” so sometimes you will see something like “x <- 2 + 5”.
16. Okay, now it is time to do some of the Bayesian tests. To do the Bayesian equivalent of a single sample t-test again zero you would use the following command: “results1 = BESTmcmc(difscores)”. The command will do some processing, then it will be done. To see the results, in this case simply type “results1” at the command prompt “>”. This will give you some of the key output, perhaps most important of which is the low and high limits of the Bayesian Credible Interval – the “mu” line “HDIhi” and “HDIlo”.
17. To see the classic plot, simply type “plot(results1)” at the command prompt and you will see the distribution with the limits plotted.
18. Now, it is really that easy. Recall that a paired samples t-test is the single samples t-test of the difference scores against zero. As such, what you did in step 16 is the Bayesian equivalent of a paired samples t-test again zero as the input was a set of difference scores!
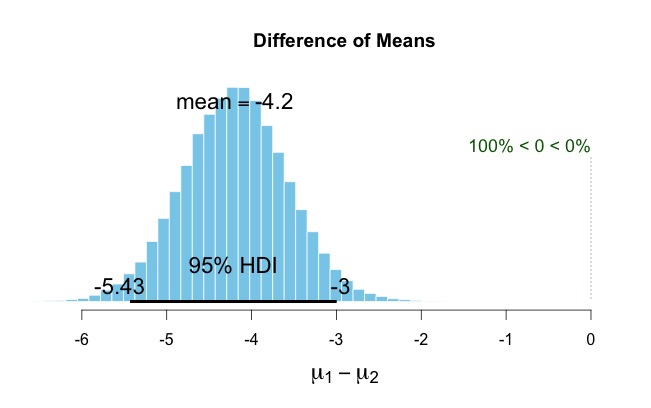
19. To do the Bayesian equivalent of an independent samples t-test, simply use the following command: “results2 = BESTmcmc(data1$V1,data1$V2)”. If you look at “results2” then you will see there is now mu1 and mu2, the HDIs for each of the two data sets. If you now plot(results2) you will see a comparison of the difference scores of the two data sets – however, note, these results are different from the above analysis “results1” because the input was two different sample populations. NOTE: Because zero is not included in the Bayesian Credible Interval for the mean difference scores you would infer these two groups are from different populations (i.e., p < 0.05 in a NHST framework). To see a complete plot of all the relevant output type “plotAll(results2)” – you may need to resize the plot window.
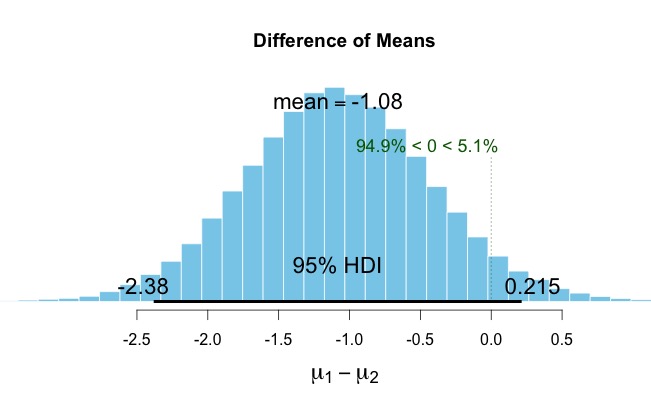
20. Now, using the above steps as a guide load “data2.txt” (i.e., data2 = read.table(‘data2.txt’)). Assume this reflects two groups as per step 19. Run the analysis and assign the results to “results3”. You should see that these groups do not differ as zero is included within the Bayesian Credible Interval range (i.e., a plot(results3) clearly shows that zero is within the distribution. Note, it is close – but it is still in the distribution.
1. OSX users. You need to install the latest version of XCode from the App store. Note, you will need to run XCode and accept the user agreement before you go any further.
2. Install R on your computer. Go to: http://cran.stat.sfu.ca/ and select the correct version for your operating system.
3. Install R Studio on your computer. Go to: https://www.rstudio.com/products/rstudio/download/
4. Install “jags” – this is a program that the BEST package needs in order to do some of the probability mathematics. Go to: http://sourceforge.net/projects/mcmc-jags/files/JAGS/4.x/
5. Open R. You should get to a command window. I have found that installing packages in R as opposed to R Studio leads to considerably greater success.
6. At the command “>” type in “install.packages(‘rjags’)” and hit enter. This will install the “rjags” package that you will need for BEST. Note, you will most likely see R installing a bunch of other packages that “rjags” needs to work. This is normal and okay.
7. At the command “>” type in “install.packages(‘BEST’)” and hit enter. This will install the “BEST” package. Note, you will most likely see R installing a bunch of other packages that “BEST” needs to work. This is normal and okay.
8. Create a directory called “R” on your desktop and put the attached sample data file, “data1.txt” in that directory (or a directory of your choice).
9. Open R Studio. (Note, this is not a full R tutorial, I will leave that for others).
10. At the command prompt, “>” type in “library(BEST)”. This tells R that you will be using the BEST library for some of your commands.
11. Next, change your working directory to the R directory in RStudio by typing “setwd("~/Desktop/R")” at the command prompt “>”.
12. Now, we will load in the sample data file (data1.txt). At the command prompt “>” type in “data1 = read.table("data1.txt")” to load the file data.txt into a structure that R calls a table. It's a matrix, but one specifically designed to work with statistical data. If you now simply type “data1” at the command prompt “>” you should see two columns (V1, V2) of 20 numbers.
13. To just look at a single column of numbers in R you isolate it by typing “data1$V1” for instance at the command prompt “>”.
14. Lets create the difference scores for this data. Type “difscores = data1$V2 – data1$V1” at the command prompt “>”. Check to see this works by typing “difscores” at the command prompt “>”.
15. As you can see, R is a bit like MATLAB or other programming environments. Anything on the left of an equals sign is an assigned variable and anything on the right is / are operations. For example, using a classic example if you type “x = 2 + 5” you will be creating a variable “x” that is equal to 7. In the original version of R “<-“ was used instead of “=” so sometimes you will see something like “x <- 2 + 5”.
16. Okay, now it is time to do some of the Bayesian tests. To do the Bayesian equivalent of a single sample t-test again zero you would use the following command: “results1 = BESTmcmc(difscores)”. The command will do some processing, then it will be done. To see the results, in this case simply type “results1” at the command prompt “>”. This will give you some of the key output, perhaps most important of which is the low and high limits of the Bayesian Credible Interval – the “mu” line “HDIhi” and “HDIlo”.
17. To see the classic plot, simply type “plot(results1)” at the command prompt and you will see the distribution with the limits plotted.
18. Now, it is really that easy. Recall that a paired samples t-test is the single samples t-test of the difference scores against zero. As such, what you did in step 16 is the Bayesian equivalent of a paired samples t-test again zero as the input was a set of difference scores!
19. To do the Bayesian equivalent of an independent samples t-test, simply use the following command: “results2 = BESTmcmc(data1$V1,data1$V2)”. If you look at “results2” then you will see there is now mu1 and mu2, the HDIs for each of the two data sets. If you now plot(results2) you will see a comparison of the difference scores of the two data sets – however, note, these results are different from the above analysis “results1” because the input was two different sample populations. NOTE: Because zero is not included in the Bayesian Credible Interval for the mean difference scores you would infer these two groups are from different populations (i.e., p < 0.05 in a NHST framework). To see a complete plot of all the relevant output type “plotAll(results2)” – you may need to resize the plot window.
20. Now, using the above steps as a guide load “data2.txt” (i.e., data2 = read.table(‘data2.txt’)). Assume this reflects two groups as per step 19. Run the analysis and assign the results to “results3”. You should see that these groups do not differ as zero is included within the Bayesian Credible Interval range (i.e., a plot(results3) clearly shows that zero is within the distribution. Note, it is close – but it is still in the distribution.