ANOVA ASSUMPTIONS
In earlier lessons you learned how to test to see whether or not two groups differed - an independent samples t-test. But what do you do if you have more than two groups?
The first case we will examine is when you have three or more independent groups and you want to see whether or not there are differences between them - the test that accomplishes this is an Analysis of Variance - a between subjects test to determine if there is a difference between three or more groups.
Analysis of Variance (ANOVA) is a complex business, at this point you need to find a textbook and read the chapter(s) on ANOVA. For a quick summary you can go HERE, but that is not really going to be enough.
Load this DATA into a new table called "data" in R Studio. You will note the first column indicates subject numbers from 1 to 150, the second column groups codes for 3 groups, and the third column actual data. Rename the columns "subject", "group", and "rt".
Lets define group as a factor. Remember how to do that?
data$group = factor(data$group)
Before we actually run an ANOVA we need to test the assumptions of this test. What are assumptions? In short, each statistical test can only be run if the data meet certain criteria. For ANOVA, there are four assumptions that you need to meet.
Assumption One: Between Group Independence. The groups are independent. Essentially, your groups cannot be related - for instance - if you are interested in studying age this is easy - a "young" group is naturally independent of groups that are "middle aged" and "elderly". This may not be as true in all instances and you need to be sure. Note, there is no statistical test for this, you need to use logic and common sense. For example, the means and variances of a group may be identical but they can be truly independent. Consider this - you are interested in how many calories a day people eat. You create a group in Berlin, Germany and Auckland, New Zealand and find they eat the same number of calories per day as reflected by the means and the variances. These groups are most likely independent but they share common statistical properties.
Assumption Two: Within Group Sampling and Independence. The members of each groups are sampled randomly and are independent of each other. This relates to research methods and is beyond the scope of this tutorial, but typically we do the best we can here.
Assumption Three: Normality. The data for each group are drawn from a normally distributed population. Actually, this is not 100%. The actual assumption is that the sampling distribution of the mean of the population from which the data is drawn is normally distributed. There is a lot of theory here, but in short, this is actually almost always true and most people have a misperception of this assumption. Most people think that the assumption means that the data itself is normally distributed which is not true at all. The confusion stems from the fact that most textbooks state something like this "If the data is normally distributed then the assumption is met". That is a true statement, if your data is normally distributed then it is extremely likely that the sampling distribution of the mean of the population the data is from is normally distributed. However, if the data is not normally distributed then it is still quite possible that the sampling distribution of the mean of the population data is normally distributed. You should discuss this one with your statistics professor if you are still confused!
In spite of this, most people like to test whether the data is normally distributed or not. Here are three ways to do this:
a. Plot Histograms for each group and assess this through visual inspection. For the above data:
par(mfcol=c(1, 3))
hist(data$rt[data$group==1])
hist(data$rt[data$group==2])
hist(data$rt[data$group==3])
b. Examine the skew and kurtosis of the data for each group. You can read more about Skewness and Kurtosis HERE and HERE, but essentially Skewness assesses how much to the left or right the distribution is pulled (0 is perfectly normal) and kurtosis assesses how flat or peaked the distribution is (3 is perfectly normal).
To test the skewness and kurtosis for the first group you would use the following commands:
install.packages("moments")
library("moments")
skewness(data$rt[data$group==1])
kurtosis(data$rt[data$group==1])
skewness(data$rt[data$group==2])
kurtosis(data$rt[data$group==2])
skewness(data$rt[data$group==3])
kurtosis(data$rt[data$group==3])
c. Use QQ plots to assess normality. On a QQ plot the data is normal if it all falls on a line. Try the following code:
qqnorm(data$rt[data$group==1])
qqline(data$rt[data$group==1])
qqnorm(data$rt[data$group==2])
qqline(data$rt[data$group==2])
qqnorm(data$rt[data$group==3])
qqline(data$rt[data$group==3])
The first case we will examine is when you have three or more independent groups and you want to see whether or not there are differences between them - the test that accomplishes this is an Analysis of Variance - a between subjects test to determine if there is a difference between three or more groups.
Analysis of Variance (ANOVA) is a complex business, at this point you need to find a textbook and read the chapter(s) on ANOVA. For a quick summary you can go HERE, but that is not really going to be enough.
Load this DATA into a new table called "data" in R Studio. You will note the first column indicates subject numbers from 1 to 150, the second column groups codes for 3 groups, and the third column actual data. Rename the columns "subject", "group", and "rt".
Lets define group as a factor. Remember how to do that?
data$group = factor(data$group)
Before we actually run an ANOVA we need to test the assumptions of this test. What are assumptions? In short, each statistical test can only be run if the data meet certain criteria. For ANOVA, there are four assumptions that you need to meet.
Assumption One: Between Group Independence. The groups are independent. Essentially, your groups cannot be related - for instance - if you are interested in studying age this is easy - a "young" group is naturally independent of groups that are "middle aged" and "elderly". This may not be as true in all instances and you need to be sure. Note, there is no statistical test for this, you need to use logic and common sense. For example, the means and variances of a group may be identical but they can be truly independent. Consider this - you are interested in how many calories a day people eat. You create a group in Berlin, Germany and Auckland, New Zealand and find they eat the same number of calories per day as reflected by the means and the variances. These groups are most likely independent but they share common statistical properties.
Assumption Two: Within Group Sampling and Independence. The members of each groups are sampled randomly and are independent of each other. This relates to research methods and is beyond the scope of this tutorial, but typically we do the best we can here.
Assumption Three: Normality. The data for each group are drawn from a normally distributed population. Actually, this is not 100%. The actual assumption is that the sampling distribution of the mean of the population from which the data is drawn is normally distributed. There is a lot of theory here, but in short, this is actually almost always true and most people have a misperception of this assumption. Most people think that the assumption means that the data itself is normally distributed which is not true at all. The confusion stems from the fact that most textbooks state something like this "If the data is normally distributed then the assumption is met". That is a true statement, if your data is normally distributed then it is extremely likely that the sampling distribution of the mean of the population the data is from is normally distributed. However, if the data is not normally distributed then it is still quite possible that the sampling distribution of the mean of the population data is normally distributed. You should discuss this one with your statistics professor if you are still confused!
In spite of this, most people like to test whether the data is normally distributed or not. Here are three ways to do this:
a. Plot Histograms for each group and assess this through visual inspection. For the above data:
par(mfcol=c(1, 3))
hist(data$rt[data$group==1])
hist(data$rt[data$group==2])
hist(data$rt[data$group==3])
b. Examine the skew and kurtosis of the data for each group. You can read more about Skewness and Kurtosis HERE and HERE, but essentially Skewness assesses how much to the left or right the distribution is pulled (0 is perfectly normal) and kurtosis assesses how flat or peaked the distribution is (3 is perfectly normal).
To test the skewness and kurtosis for the first group you would use the following commands:
install.packages("moments")
library("moments")
skewness(data$rt[data$group==1])
kurtosis(data$rt[data$group==1])
skewness(data$rt[data$group==2])
kurtosis(data$rt[data$group==2])
skewness(data$rt[data$group==3])
kurtosis(data$rt[data$group==3])
c. Use QQ plots to assess normality. On a QQ plot the data is normal if it all falls on a line. Try the following code:
qqnorm(data$rt[data$group==1])
qqline(data$rt[data$group==1])
qqnorm(data$rt[data$group==2])
qqline(data$rt[data$group==2])
qqnorm(data$rt[data$group==3])
qqline(data$rt[data$group==3])
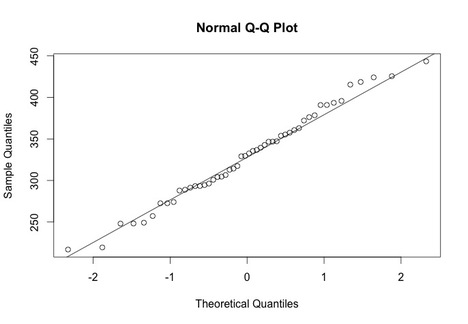
The data here is all pretty close to the line, which suggests that the data is normal.
d. Use a formal statistical test that assesses normality like the Shapiro - Wilk Test.
shapiro.test(data$rt[data$group==1])
shapiro.test(data$rt[data$group==2])
shapiro.test(data$rt[data$group==3])
If the p value of this test is not significant, i.e., p > 0.05, then it suggests that the data is normally distributed.
Assumption Four: Homogeneity of Variance. ANOVA assumes that the variances of all groups are equivalent. There are three ways to test this.
a. Plot Histograms (ensure the number of bins and axes are the same) and visually ensure that the variances are roughly equivalent. See above.
b. Compute the variances for each group:
var(data$rt[data$group==1])
var(data$rt[data$group==2])
var(data$rt[data$group==3])
A general rule of thumb is that if the smallest variance is within 4 magnitudes of the largest variance then the assumption is met. In other words varmax < 4 x varmin.
c. Use a statistical test of the assumption. The Bartlett Test tests the assumption directly and returns a p value. If the p value is significant, p < 0.05, then the assumption is not met. Dealing with a violation of the assumption is beyond this assignment, but you do need to be aware if any of the assumptions are violated.
bartlett.test(data$rt~data$group)
Alternatively, you could use an alternative test such as Levene's Test.
leveneTest(data$rt~data$group)
shapiro.test(data$rt[data$group==1])
shapiro.test(data$rt[data$group==2])
shapiro.test(data$rt[data$group==3])
If the p value of this test is not significant, i.e., p > 0.05, then it suggests that the data is normally distributed.
Assumption Four: Homogeneity of Variance. ANOVA assumes that the variances of all groups are equivalent. There are three ways to test this.
a. Plot Histograms (ensure the number of bins and axes are the same) and visually ensure that the variances are roughly equivalent. See above.
b. Compute the variances for each group:
var(data$rt[data$group==1])
var(data$rt[data$group==2])
var(data$rt[data$group==3])
A general rule of thumb is that if the smallest variance is within 4 magnitudes of the largest variance then the assumption is met. In other words varmax < 4 x varmin.
c. Use a statistical test of the assumption. The Bartlett Test tests the assumption directly and returns a p value. If the p value is significant, p < 0.05, then the assumption is not met. Dealing with a violation of the assumption is beyond this assignment, but you do need to be aware if any of the assumptions are violated.
bartlett.test(data$rt~data$group)
Alternatively, you could use an alternative test such as Levene's Test.
leveneTest(data$rt~data$group)